백준 11729


내코드

우선 n개의 원판을 큰 순서대로 n부터 이름붙여 생각했다. 예를 들어 4개의 원판이 있다면 1장대에는 밑에서부터 4, 3, 2, 1 원판이 쌓여있을 것이다. 장대의 모든 원판들을 옮기는 과정을 원판들 중 가장 큰 원판을 기준으로 생각했다. 만약 1장대의 1~4원판을 모두 3장대로 옮기기 위해서는 4원판이 3장대의 가장 아래로 이동해야 할 것이다. 그러기위해서는 1~3원판이 먼저 2장대로 모두 이동후 4원판이 3장대로 이동해야 할 것이고, 그 후 1~3원판이 3장대로 이동한다면 모든 원판이 이동을 완료할 것이다.

또 1~3원판이 모두 2장대로 이동하기 위해서는 가장 큰 원판인 3원판이 2장대의 가장 아래로 이동해야 할 것이다. 그러기 위해서는 1~2원판이 먼저 3장대로 모두 이동후 3원판이 2장대로 이동해야 할 것이고, 그 후 1~2원판이 2장대로 이동하면 1~3원판이 모두 2장대로 이동을 완료한다.

이를 그림이 아닌 식으로 알아보기 쉽게 표현하기 위해서 임시로 hanoi(name, to, from)은 name 이하 모든 원판이 from에서 to로 이동하는 것으로, (name, to, from)은 name 원판이 from에서 to로 이동하는 것으로 생각했다. 예를 들어 hanoi(4,3,1)은 4이하 모든 원판(4,3,2,1)이 1장대에서 3장대로 이동하는 것이다. 또 (4,3,1)은 4원판 한개가 1장대에서 4장대로 이동하는 것이다.

만약 4이하 모든 원판을 1장대에서 3장대로 옮기고 싶다면 hanoi(4,3,1)을 사용해 표현할 수 있다. 그림에서 봤듯이 4이하 모든 원판을 1장대에서 3장대로 옮기기 위해선 먼저 3이하 모든 원판을 1장대에서 2장대로 옮긴후(hanoi(3,2,1), 4원판을 1장대에서 3장대로 옮기고(4,3,1), 또 3이하 모든 원판을 2장대에서 3장대로 옮겨야한다(hanoi(3,3,2). 이를 계속 반복해서 생각하여 정리하면 위의 그림과 같이 정리할 수 있다.
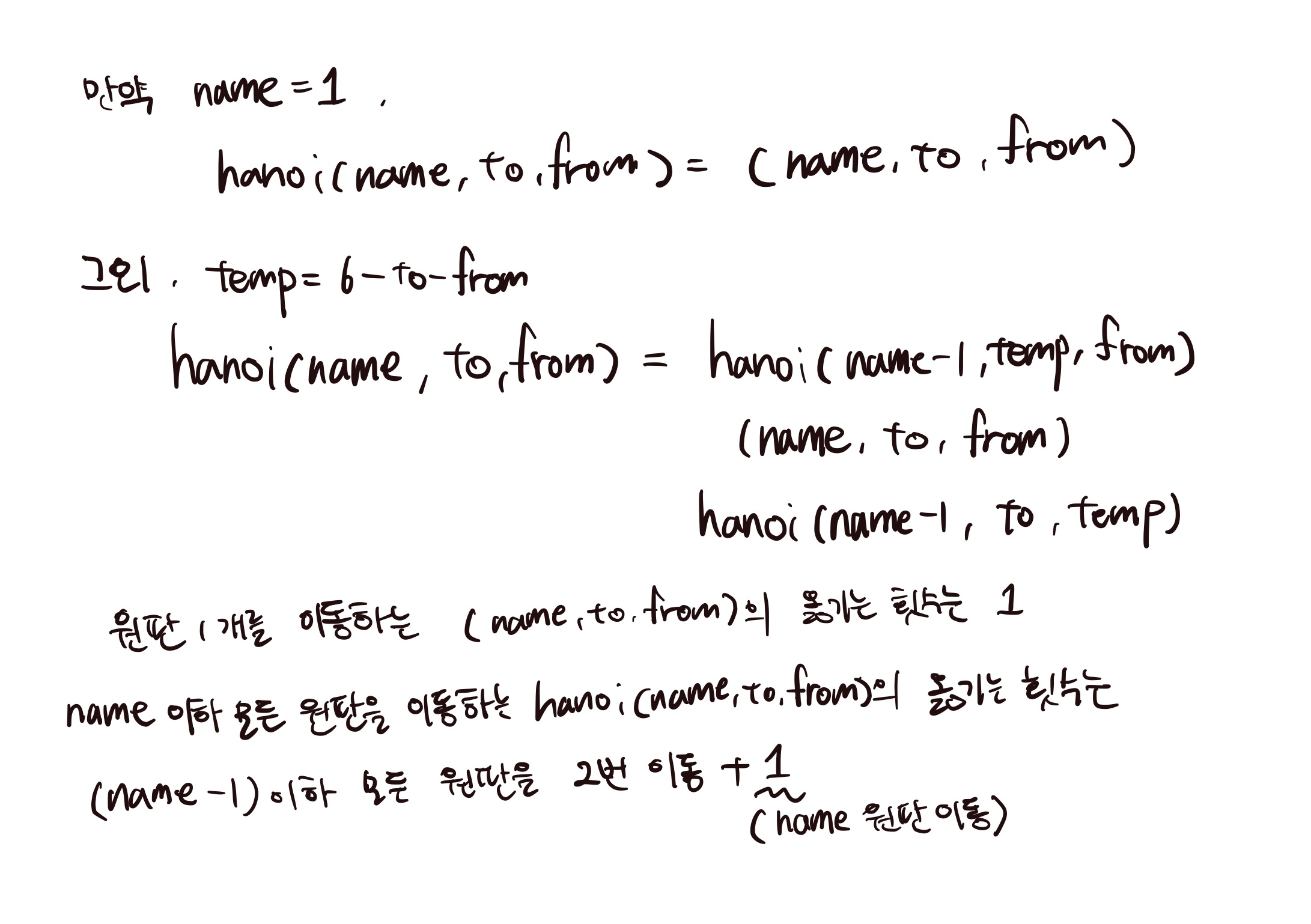
정리한 것을 기반으로 식의 관계를 유추해보면 name이하의 모든 원판을 from에서 to로 옮기기위해서는 (name-1)이하의 모든 원판을 from에서 temp(to, from이 아닌 나머지 장대)로 옮긴 후(=hanoi(name-1,temp,from)), name원판을 from에서 to로 옮기고(=(name,to,from)), name-1이하의 모든 원판을 temp에서 from으로 옮긴다는 것을 알 수 있다(=(hanoi(name-1,to,temp)). 만약 name이 1이라면 1이하의 원판은 총 1개이기에 1이하의 모든 원판을 옮기는 것(=hanoi(1, to, from))은 1원판을 옮기는 것(=(1,to,from))과 동일한 것을 알 수 있다.
이를 원판을 옮기는 횟수를 기준으로 정리해본다면 원판 1개만을 이동시키는 (name, to, from)의 경우 옮기는 횟수가 1이 된다. name이하의 모든 원판을 이동시키는 hanoi(name, to, from)의 옮기는 횟수는 (name-1)이하 모든 원판을 총 2번 이동하는 것+ name원판이 이동하는 1 인 것을 알 수 있다.
아래는 이를 기반으로 작성한 코드이다.
(위에서 hanoi(name, to, from)은 hanoiTrace로 이름을 변경하였고, hanoiCount는 원판을 옮기는 횟수를 구하는 함수이다.)
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
void hanoiTrace(int name, int to, int from) {
int temp = 6 - to - from;
if (name == 1) {
printf("%d %d\n", from, to);
//printf("(name: %d, to: %d, from: %d)\n", name, to, from);
}
else {
hanoiTrace(name - 1, temp, from);
printf("%d %d\n", from, to);
//printf("(name: %d, to: %d, from: %d)\n", name, to, from);
hanoiTrace(name - 1, to, temp);
}
}
int hanoiCount(int c) {
if (c == 1) {
return 1;
}
else {
return 1 + 2*(hanoiCount(c - 1));
}
}
int main() {
int n;
scanf("%d", &n);
int result = hanoiCount(n);
printf("%d\n", result);
hanoiTrace(n, 3, 1);
return 0;
}
'C' 카테고리의 다른 글
| [C]백준 10.재귀: 10870 (0) | 2022.01.16 |
|---|---|
| [C]백준 10.재귀: 10872 (0) | 2022.01.16 |
| [C]백준 09.기본수학2: 1002 (0) | 2022.01.15 |
| [C]백준 09.기본수학2: 3053 (0) | 2022.01.15 |
| [C]백준 09.기본수학2: 4153 (0) | 2022.01.15 |



